How Does The 100% Rule Affect The Risk Register?

Economic science theory

Adventure aversion (carmine) contrasted to risk neutrality (xanthous) and hazard loving (orangish) in different settings. Left graph: A run a risk averse utility function is concave (from below), while a risk loving utility function is convex. Center graph: In standard deviation-expected value infinite, run a risk averse indifference curves are upwards sloped. Right graph: With fixed probabilities of two alternative states one and 2, chance balky indifference curves over pairs of state-contingent outcomes are convex.

In economic science and finance, risk aversion is the trend of people to adopt outcomes with low uncertainty to those outcomes with high dubiousness, even if the average outcome of the latter is equal to or higher in budgetary value than the more certain outcome.^[1] Risk aversion explains the inclination to agree to a situation with a more predictable, just perhaps lower payoff, rather than some other situation with a highly unpredictable, but perchance higher payoff. For example, a risk-averse investor might cull to put their coin into a depository financial institution account with a depression just guaranteed interest rate, rather than into a stock that may take high expected returns, but also involves a chance of losing value.

Instance [edit]

Utility function of a gamble-averse (risk-avoiding) individual

Utility function of a risk-neutral individual

Utility part of a adventure-loving (adventure-seeking) individual

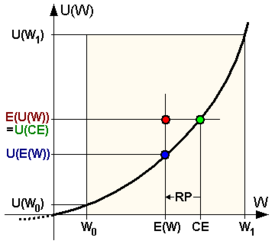
CE – Certainty equivalent; East(U(W)) – Expected value of the utility (expected utility) of the uncertain payment W; E(W) – Expected value of the uncertain payment; U(CE) – Utility of the certainty equivalent; U(Due east(West)) – Utility of the expected value of the uncertain payment; U(W₀) – Utility of the minimal payment; U(W₁) – Utility of the maximal payment; W₀ – Minimal payment; W_i – Maximal payment; RP – Adventure premium

A person is given the choice between 2 scenarios: one with a guaranteed payoff, and one with a risky payoff with same average value. In the former scenario, the person receives $50. In the uncertain scenario, a money is flipped to decide whether the person receives $100 or nothing. The expected payoff for both scenarios is $50, meaning that an individual who was insensitive to risk would non care whether they took the guaranteed payment or the take a chance. However, individuals may take dissimilar take a chance attitudes.^{[2] [three] [iv]}

A person is said to exist:

• take a chance balky (or risk avoiding) - if they would accept a certain payment (certainty equivalent) of less than $50 (for example, $forty), rather than taking the gamble and possibly receiving nothing.
• adventure neutral – if they are indifferent between the bet and a certain $50 payment.
• run a risk loving (or run a risk seeking) – if they would take the bet even when the guaranteed payment is more than $50 (for instance, $60).

The average payoff of the gamble, known as its expected value, is $fifty. The smallest dollar amount that an individual would be indifferent to spending on a hazard or guarantee is called the certainty equivalent, which is as well used equally a mensurate of risk aversion. An private that is chance averse has a certainty equivalent that is smaller than the prediction of uncertain gains. The risk premium is the difference betwixt the expected value and the certainty equivalent. For hazard-averse individuals, risk premium is positive, for adventure-neutral persons it is zero, and for risk-loving individuals their risk premium is negative.

Utility of money [edit]

In expected utility theory, an agent has a utility part u(c) where c represents the value that he might receive in coin or goods (in the above example c could exist $0 or $40 or $100).

The utility part u(c) is defined simply upward to positive affine transformation – in other words, a abiding could be added to the value of u(c) for all c, and/or u(c) could be multiplied by a positive abiding factor, without affecting the conclusions.

An agent possesses risk aversion if and just if the utility function is concave. For instance u(0) could be 0, u(100) might be 10, u(40) might be v, and for comparing u(50) might exist 6.

The expected utility of the to a higher place bet (with a fifty% take a chance of receiving 100 and a 50% chance of receiving 0) is

${\displaystyle Due east(u)=(u(0)+u(100))/2}$ ,

and if the person has the utility function with u(0)=0, u(xl)=5, and u(100)=10 and then the expected utility of the bet equals five, which is the same equally the known utility of the amount 40. Hence the certainty equivalent is twoscore.

The run a risk premium is ($fifty minus $twoscore)=$10, or in proportional terms

${\displaystyle (\$50-\$forty)/\$forty}$

or 25% (where $50 is the expected value of the risky bet: ( ${\displaystyle {\tfrac {i}{2}}0+{\tfrac {1}{2}}100}$ ). This risk premium ways that the person would be willing to sacrifice as much as $10 in expected value in lodge to achieve perfect certainty near how much coin will exist received. In other words, the person would exist indifferent between the bet and a guarantee of $twoscore, and would adopt annihilation over $40 to the bet.

In the case of a wealthier individual, the risk of losing $100 would be less significant, and for such modest amounts his utility function would be probable to exist almost linear. For instance, if u(0) = 0 and u(100) = 10, then u(40) might be iv.02 and u(50) might be five.01.

The utility function for perceived gains has two key properties: an upward slope, and concavity. (i) The upwardly gradient implies that the person feels that more is meliorate: a larger amount received yields greater utility, and for risky bets the person would prefer a bet which is first-order stochastically ascendant over an alternative bet (that is, if the probability mass of the 2nd bet is pushed to the right to class the first bet, then the start bet is preferred). (ii) The concavity of the utility function implies that the person is risk averse: a sure amount would always be preferred over a risky bet having the same expected value; moreover, for risky bets the person would prefer a bet which is a mean-preserving contraction of an alternative bet (that is, if some of the probability mass of the commencement bet is spread out without altering the hateful to form the second bet, then the outset bet is preferred).

Measures of hazard aversion under expected utility theory [edit]

In that location are multiple measures of the take chances aversion expressed past a given utility function. Several functional forms oftentimes used for utility functions are expressed in terms of these measures.

Absolute adventure aversion [edit]

The college the curvature of ${\displaystyle u(c)}$ , the higher the take a chance aversion. Notwithstanding, since expected utility functions are non uniquely divers (are defined only up to affine transformations), a measure that stays abiding with respect to these transformations is needed rather than just the second derivative of ${\displaystyle u(c)}$ . 1 such measure is the Arrow–Pratt measure of absolute risk aversion (ARA), after the economists Kenneth Arrow and John Westward. Pratt,^{[5] [six]} also known as the coefficient of accented risk disfavor, defined every bit

${\displaystyle A(c)=-{\frac {u''(c)}{u'(c)}}}$

where ${\displaystyle u'(c)}$ and ${\displaystyle u''(c)}$ announce the outset and second derivatives with respect to ${\displaystyle c}$ of ${\displaystyle u(c)}$ . For instance, if ${\displaystyle u(c)=\alpha +\beta ln(c),}$ so ${\displaystyle u'(c)=\beta /c}$ and ${\displaystyle u''(c)=-\beta /c^{2},}$ and so ${\displaystyle A(c)=i/c.}$ Note how ${\displaystyle A(c)}$ does not depend on ${\displaystyle \alpha }$ and ${\displaystyle \beta ,}$ so affine transformations of ${\displaystyle u(c)}$ do not change it.

The post-obit expressions relate to this term:

${\displaystyle A(c)=-{\frac {u''(c)}{u'(c)}}={\frac {1}{ac+b}}}$

The solution to this differential equation (omitting additive and multiplicative constant terms, which do not touch on the behavior unsaid past the utility function) is:

${\displaystyle u(c)={\frac {(c-c_{due south})^{ane-R}}{1-R}}}$

where ${\displaystyle R=1/a}$ and ${\displaystyle c_{s}=-b/a}$ . Note that when ${\displaystyle a=0}$ , this is CARA, as ${\displaystyle A(c)=ane/b=const}$ , and when ${\displaystyle b=0}$ , this is CRRA (run into below), every bit ${\displaystyle cA(c)=1/a=const}$ . Run into ^[7]

• Decreasing/increasing absolute take a chance aversion (DARA/IARA) is present if ${\displaystyle A(c)}$ is decreasing/increasing. Using the above definition of ARA, the following inequality holds for DARA:

${\displaystyle {\frac {\partial A(c)}{\partial c}}=-{\frac {u'(c)u'''(c)-[u''(c)]^{2}}{[u'(c)]^{2}}}<0}$

and this can concord but if ${\displaystyle u'''(c)>0}$ . Therefore, DARA implies that the utility role is positively skewed; that is, ${\displaystyle u'''(c)>0}$ .^[8] Analogously, IARA tin can be derived with the opposite directions of inequalities, which permits merely does not require a negatively skewed utility function ( ${\displaystyle u'''(c)<0}$ ). An example of a DARA utility function is ${\displaystyle u(c)=\log(c)}$ , with ${\displaystyle A(c)=i/c}$ , while ${\displaystyle u(c)=c-\blastoff c^{two},}$ ${\displaystyle \blastoff >0}$ , with ${\displaystyle A(c)=2\blastoff /(i-ii\alpha c)}$ would represent a quadratic utility function exhibiting IARA.

• Experimental and empirical show is by and large consistent with decreasing absolute risk aversion.^[9]
• Contrary to what several empirical studies take causeless, wealth is non a skilful proxy for take chances aversion when studying gamble sharing in a principal-agent setting. Although ${\displaystyle A(c)=-{\frac {u''(c)}{u'(c)}}}$ is monotonic in wealth nether either DARA or IARA and constant in wealth nether CARA, tests of contractual risk sharing relying on wealth as a proxy for absolute run a risk aversion are ordinarily not identified.^[ten]

Relative run a risk aversion [edit]

The Arrow–Pratt measure of relative adventure aversion (RRA) or coefficient of relative take a chance aversion is defined as^[11]

${\displaystyle R(c)=cA(c)={\frac {-cu''(c)}{u'(c)}}}$ .

Unlike ARA whose units are in $^−one, RRA is a dimension-less quantity, which allows it to be applied universally. Similar for absolute chance aversion, the corresponding terms constant relative risk disfavor (CRRA) and decreasing/increasing relative risk aversion (DRRA/IRRA) are used. This measure has the advantage that information technology is nevertheless a valid measure out of risk aversion, fifty-fifty if the utility office changes from risk averse to take a chance loving as c varies, i.e. utility is not strictly convex/concave over all c. A abiding RRA implies a decreasing ARA, but the reverse is not always true. As a specific case of constant relative run a risk aversion, the utility function ${\displaystyle u(c)=\log(c)}$ implies RRA = one.

In intertemporal pick issues, the elasticity of intertemporal substitution often cannot be disentangled from the coefficient of relative gamble aversion. The isoelastic utility function

${\displaystyle u(c)={\frac {c^{1-\rho }-1}{1-\rho }}}$

exhibits constant relative risk disfavor with ${\displaystyle R(c)=\rho }$ and the elasticity of intertemporal exchange ${\displaystyle \varepsilon _{u(c)}=1/\rho }$ . When ${\displaystyle \rho =1,}$ using l'Hôpital's rule shows that this simplifies to the case of log utility, u(c) = log c, and the income result and exchange effect on saving exactly showtime.

A time-varying relative risk aversion can be considered.^[12]

Implications of increasing/decreasing absolute and relative risk disfavor [edit]

The most straightforward implications of increasing or decreasing absolute or relative risk disfavor, and the ones that motivate a focus on these concepts, occur in the context of forming a portfolio with one risky asset and one hazard-free asset.^{[5] [6]} If the person experiences an increment in wealth, he/she will choose to increment (or go on unchanged, or decrease) the number of dollars of the risky nugget held in the portfolio if absolute gamble aversion is decreasing (or constant, or increasing). Thus economists avoid using utility functions such as the quadratic, which exhibit increasing absolute risk aversion, because they take an unrealistic behavioral implication.

Similarly, if the person experiences an increase in wealth, he/she will choose to increase (or keep unchanged, or decrease) the fraction of the portfolio held in the risky asset if relative risk aversion is decreasing (or constant, or increasing).

In one model in monetary economic science, an increase in relative risk disfavor increases the impact of households' money holdings on the overall economy. In other words, the more than the relative gamble aversion increases, the more money demand shocks will impact the economy.^[13]

Portfolio theory [edit]

In modern portfolio theory, risk disfavor is measured as the additional expected reward an investor requires to have additional risk. If an investor is take a chance-averse, they will invest in multiple uncertain assets, merely but when the predicted return on a portfolio that is uncertain is greater than the predicted return on one that is not uncertain will the investor will prefer the old.^[i] Here, the risk-return spectrum is relevant, as it results largely from this type of chance disfavor. Here take chances is measured every bit the standard deviation of the return on investment, i.eastward. the square root of its variance. In advanced portfolio theory, different kinds of take a chance are taken into consideration. They are measured every bit the n-th root of the northward-th central moment. The symbol used for run a risk disfavor is A or A_n.

${\displaystyle A={\frac {dE(c)}{d\sigma }}}$

${\displaystyle A_{due north}={\frac {dE(c)}{d{\sqrt[{n}]{\mu _{n}}}}}}$

Limitations of expected utility treatment of take chances aversion [edit]

Using expected utility theory'due south approach to chance aversion to analyze small stakes decisions has come under criticism. Matthew Rabin has showed that a risk-averse, expected-utility-maximizing individual who,

from any initial wealth level [...] turns down gambles where she loses $100 or gains $110, each with 50% probability [...] volition plough down fifty–50 bets of losing $one,000 or gaining whatever sum of money. ^[14]

Rabin criticizes this implication of expected utility theory on grounds of implausibility—individuals who are run a risk averse for small gambles due to diminishing marginal utility would exhibit extreme forms of adventure aversion in risky decisions nether larger stakes. I solution to the problem observed past Rabin is that proposed by prospect theory and cumulative prospect theory, where outcomes are considered relative to a reference point (usually the status quo), rather than considering only the terminal wealth.

Another limitation is the reflection issue, which demonstrates the reversing of chance aversion. This effect was first presented by Kahneman and Tversky as a part of the prospect theory, in the behavioral economic science domain. The reflection effect is an identified pattern of opposite preferences between negative as opposed to positive prospects: people tend to avoid hazard when the hazard is between gains, and to seek risks when the take a chance is between losses.^[xv] For example, nigh people prefer a certain gain of iii,000 to an fourscore% run a risk of a gain of four,000. When posed the same problem, but for losses, almost people prefer an 80% chance of a loss of 4,000 to a certain loss of iii,000.

The reflection effect (too as the certainty effect) is inconsistent with the expected utility hypothesis. It is assumed that the psychological principle which stands backside this kind of beliefs is the overweighting of certainty. Options which are perceived as certain are over-weighted relative to uncertain options. This pattern is an indication of risk-seeking behavior in negative prospects and eliminates other explanations for the certainty issue such equally aversion for dubiety or variability.^[15]

The initial findings regarding the reflection effect faced criticism regarding its validity, as it was claimed that in that location are insufficient evidence to support the upshot on the private level. Afterwards, an extensive investigation revealed its possible limitations, suggesting that the issue is about prevalent when either small or large amounts and farthermost probabilities are involved.^{[16] [17]}

In the encephalon [edit]

Attitudes towards risk have attracted the interest of the field of neuroeconomics and behavioral economic science. A 2009 written report by Christopoulos et al. suggested that the activity of a specific brain expanse (right inferior frontal gyrus) correlates with risk aversion, with more risk averse participants (i.eastward. those having higher chance premia) also having higher responses to safer options.^[xviii] This result coincides with other studies,^{[18] [nineteen]} that prove that neuromodulation of the same area results in participants making more or less risk averse choices, depending on whether the modulation increases or decreases the activity of the target expanse.

Public understanding and risk in social activities [edit]

In the real world, many government agencies, e.g. Health and Safety Executive, are fundamentally risk-averse in their mandate. This oftentimes means that they demand (with the power of legal enforcement) that risks exist minimized, even at the toll of losing the utility of the risky activeness. It is of import to consider the opportunity cost when mitigating a risk; the price of not taking the risky activity. Writing laws focused on the risk without the remainder of the utility may misrepresent society's goals. The public agreement of risk, which influences political decisions, is an expanse which has recently been recognised as deserving focus. In 2007 Cambridge Academy initiated the Winton Professorship of the Public Understanding of Risk, a office described as outreach rather than traditional academic enquiry past the holder, David Spiegelhalter.^[20]

Children [edit]

Children'south services such as schools and playgrounds take go the focus of much risk-averse planning, meaning that children are often prevented from benefiting from activities that they would otherwise accept had. Many playgrounds have been fitted with impact-absorbing matting surfaces. However, these are only designed to save children from death in the instance of direct falls on their heads and do non achieve their main goals.^[21] They are expensive, meaning that less resources are bachelor to benefit users in other ways (such as building a playground closer to the child'southward dwelling house, reducing the risk of a road traffic accident on the way to it), and—some fence—children may attempt more unsafe acts, with confidence in the artificial surface. Shiela Sage, an early years schoolhouse counselor, observes "Children who are only always kept in very safe places, are not the ones who are able to solve issues for themselves. Children need to take a certain amount of risk taking ... then they'll know how to get out of situations."^{[22] [ citation needed ]}

Game shows and investments [edit]

One experimental study with pupil-discipline playing the game of the Goggle box show Deal or No Deal finds that people are more hazard averse in the limelight than in the anonymity of a typical behavioral laboratory. In the laboratory treatments, subjects fabricated decisions in a standard, computerized laboratory setting as typically employed in behavioral experiments. In the limelight treatments, subjects made their choices in a false game bear witness environs, which included a live audience, a game testify host, and video cameras.^[23] In line with this, studies on investor beliefs notice that investors trade more than and more speculatively after switching from phone-based to online trading^{[24] [25]} and that investors tend to keep their cadre investments with traditional brokers and use a pocket-size fraction of their wealth to speculate online.^[26]

See likewise [edit]

• Ambiguity aversion
• Disinterestedness premium puzzle
• Investor profile
• Loss disfavor
• Marginal utility
• Neuroeconomics
• Optimism bias
• Problem gambling, a contrary beliefs
• Prudence in economics and finance
• Take a chance premium
• St. Petersburg paradox
• Statistical risk
• Doubt avoidance, which is dissimilar, equally incertitude is not the same as chance
• Utility

References [edit]

1. ^ ^{a b} Werner, Jan (2008). "Run a risk Disfavor". The New Palgrave Dictionary of Economics. pp. 1–6. doi:10.1057/978-1-349-95121-5_2741-1. ISBN978-1-349-95121-5.
2. ^ Mr Lev Virine; Mr Michael Trumper (28 October 2013). ProjectThink: Why Expert Managers Make Poor Project Choices. Gower Publishing, Ltd. ISBN978-1-4724-0403-ix.
3. ^ David Hillson; Ruth Murray-Webster (2007). Understanding and Managing Risk Attitude. Gower Publishing, Ltd. ISBN978-0-566-08798-i.
4. ^ Adhikari, Binay Kumar; Agrawal, Anup (June 2016). "Does local religiosity affair for depository financial institution run a risk-taking?". Journal of Corporate Finance. 38: 272–293. doi:ten.1016/j.jcorpfin.2016.01.009.
5. ^ ^{a b} Arrow, K. J. (1965). "Aspects of the Theory of Risk Bearing". The Theory of Take a chance Disfavor. Helsinki: Yrjo Jahnssonin Saatio. Reprinted in: Essays in the Theory of Chance Bearing, Markham Publ. Co., Chicago, 1971, xc–109.
6. ^ ^{a b} Pratt, John Due west. (January 1964). "Risk Aversion in the Small and in the Big". Econometrica. 32 (i/2): 122–136. doi:10.2307/1913738. JSTOR 1913738.
7. ^ "Zender's lecture notes".
8. ^ Levy, Haim (2006). Stochastic Authorisation: Investment Determination Making under Doubt (2nd ed.). New York: Springer. ISBN978-0-387-29302-8.
9. ^ Friend, Irwin; Blume, Marshall (1975). "The Need for Risky Assets". American Economic Review. 65 (5): 900–922. JSTOR 1806628.
10. ^ Bellemare, Marc F.; Brown, Zachary South. (Jan 2010). "On the (Mis)Use of Wealth as a Proxy for Risk Disfavor". American Periodical of Agricultural Economic science. 92 (i): 273–282. doi:x.1093/ajae/aap006. hdl:10161/7006. S2CID 59290774.
11. ^ Simon, Carl and Lawrence Blume (2006). Mathematics for Economists (Educatee ed.). Viva Norton. p. 363. ISBN978-81-309-1600-two.
12. ^ Benchimol, Jonathan (March 2014). "Risk aversion in the Eurozone". Research in Economics. 68 (1): 39–56. doi:ten.1016/j.rie.2013.11.005. S2CID 153856059.
13. ^ Benchimol, Jonathan; Fourçans, André (March 2012). "Coin and take a chance in a DSGE framework: A Bayesian application to the Eurozone". Journal of Macroeconomics. 34 (1): 95–111. doi:x.1016/j.jmacro.2011.10.003. S2CID 153669907.
14. ^ Rabin, Matthew (2000). "Risk Aversion and Expected-Utility Theory: A Calibration Theorem". Econometrica. 68 (v): 1281–1292. CiteSeerX10.1.1.295.4269. doi:10.1111/1468-0262.00158.
15. ^ ^{a b} Kahneman, Daniel; Tversky, Amos (March 1979). "Prospect Theory: An Analysis of Conclusion under Chance". Econometrica. 47 (two): 263. CiteSeerX10.i.1.407.1910. doi:x.2307/1914185. JSTOR 1914185.
16. ^ Hershey, John C.; Schoemaker, Paul J.H. (June 1980). "Prospect theory's reflection hypothesis: A critical test". Organizational Beliefs and Man Functioning. 25 (3): 395–418. doi:10.1016/0030-5073(lxxx)90037-9.
17. ^ Battalio, RaymondC.; Kagel, JohnH.; Jiranyakul, Komain (March 1990). "Testing betwixt culling models of choice under incertitude: Some initial results". Journal of Hazard and Uncertainty. 3 (one). doi:x.1007/BF00213259. S2CID 154386816.
18. ^ ^{a b} Knoch, Daria; Gianotti, Lorena R. R.; Pascual-Leone, Alvaro; Treyer, Valerie; Regard, Marianne; Hohmann, Martin; Brugger, Peter (14 June 2006). "Disruption of Right Prefrontal Cortex by Depression-Frequency Repetitive Transcranial Magnetic Stimulation Induces Gamble-Taking Behavior". The Journal of Neuroscience. 26 (24): 6469–6472. doi:10.1523/JNEUROSCI.0804-06.2006. PMC6674035. PMID 16775134.
19. ^ Fecteau, Shirley; Pascual-Leone, Alvaro; Zald, David H.; Liguori, Paola; Théoret, Hugo; Boggio, Paulo S.; Fregni, Felipe (vi June 2007). "Activation of Prefrontal Cortex by Transcranial Straight Current Stimulation Reduces Appetite for Risk during Ambiguous Determination Making". The Periodical of Neuroscience. 27 (23): 6212–6218. doi:10.1523/JNEUROSCI.0314-07.2007. PMC6672163. PMID 17553993.
20. ^ Spiegelhalter, David (2009). "Don's Diary" (PDF). CAM – the Cambridge Alumni Magazine. The University of Cambridge Evolution Office. 58: 3. Archived from the original (PDF) on March ix, 2013.
21. ^ Gill, Tim (2007). No fear: Growing up in a Run a risk Balky society (PDF). Calouste Gulbenkian Foundation. p. 81. ISBN9781903080085. Archived from the original (PDF) on 2009-03-06.
22. ^ Sue Durant, Sheila Sage (x January 2006). Early Years – The Outdoor Surround. Teachers TV.
23. ^ Baltussen, Guido; van den Assem, Martijn J.; van Dolder, Dennie (May 2016). "Risky Option in the Limelight". Review of Economics and Statistics. 98 (2): 318–332. doi:10.1162/REST_a_00505. S2CID 57561510. SSRN 2057134.
24. ^ Hairdresser, Brad M; Odean, Terrance (1 February 2001). "The Internet and the Investor". Periodical of Economic Perspectives. 15 (i): 41–54. doi:ten.1257/jep.15.1.41.
25. ^ Hairdresser, Brad; Odean, Terrance (2002). "Online Investors: Do the Slow Die Get-go?". Review of Financial Studies. 15 (2): 455–488. CiteSeerX10.1.1.46.6569. doi:ten.1093/rfs/15.ii.455.
26. ^ Konana, Prabhudev; Balasubramanian, Sridhar (May 2005). "The Social–Economic–Psychological model of technology adoption and usage: an awarding to online investing". Decision Support Systems. 39 (3): 505–524. doi:10.1016/j.dss.2003.12.003.

U.Sankar (1971), A Utility Part for Wealth for a Risk Averter, Journal of Economical Theory.

External links [edit]

• Zevelev, Albert A. (3 February 2014). "Closed Grade Solutions in Economics". SSRN 2354226.
• Rabin, Matthew (2000). "Diminishing Marginal Utility of Wealth Cannot Explain Risk Aversion". In Kahneman, Daniel; Tversky, Amos (eds.). Choices, Values, and Frames. Cambridge University Press. pp. 202–208. ISBN978-0-521-62749-8.
• "Monkey concern-sense". The Economist. 23 June 2005.
• Arrow-Pratt Measure on Near.com:Economics
• Blackburn, Douglas W.; Ukhov, Andrey (i May 2008). "Private vs. Amass Preferences: The Case of a Small Fish in a Big Swimming". SSRN 941126.
• The benefit of utilities: a plausible caption for small risky parts in the portfolio

Source: https://en.wikipedia.org/wiki/Risk_aversion

Posted by: tobiaswenscipt.blogspot.com

Share this post